Evaluating the impact of mentorship programs
Posted on Fri 04 June 2021 in life
One initiative that I have been working on for the past year at MIT is the EECS Graduate Application Assistance Program (EECS GAAP), both as an organizer and as a mentor. EECS GAAP is a program that pairs underrepresented applicants to the MIT EECS department with graduate student mentors.
This program is motivated by the understanding that some applicants to graduate school are privileged to have networks of experienced mentors who can give them advice about applying to different programs and feedback on their application materials. This mentorship might be the "secret sauce" that allows applicants to put the right spin on their application. Meanwhile, underrepresented students usually have fewer mentorship opportunities even if they have just as strong of a CV. Can we level the playing field by connecting these students with mentors?
In EECS GAAP, applicants and their mentors worked closely together during the Fall 2020 application period on their application strategy, statement of purpose, CV, and other materials to best tell the story of their existing experience and skills to the admissions committee. Though we did not have enough mentors for all students interested in our program, we provided additional support for these students such as group mentoring sessions, short office hour-style appointments, and an "insider's guide" to the application.
Together with several other student leaders and many volunteers, we have recently wrapped up our first year. I encourage you to learn more about our program by reading our launch post or the press coverage from MIT News. Our program is one of many that have been sprouting up around the US in computer science departments and others, and there is a long history of mentorship programs in many academic arenas.
Today, I want to write about one technical problem that arises in mentorship programs. That is, do they work? And can we provide a method to answer this question quantitatively.
Do they work?
More specifically, do they actually improve the graduate admissions outcomes of applicants?
To be sure, there are many benefits of mentorship programs to applicants and mentors beyond headline admissions outcomes. But both applicants and their mentors invest a significant amount of time and effort in working together. For applicants, they have to bring mentors into their confidence to share their background and the materials that go into their application, some of which may be quite personal. For mentors, they have to carve time out of their busy research schedules to read and edit statements of purpose and try to provide good advice. At the end of the day, we hope that these investments are worth it in terms of addressing some of the inequities that lead some students to be underrepresented in certain academic spaces. The opportunity cost is extremely high and admissions outcomes should be the driving consideration.
While at first it might seem clear that supplementing a student with expert guidance would improve their outcomes, it's not obvious that we would actually see a strong impact. Students who seek out and choose to participate in mentorship programs may already be more ambitious and stronger candidates. And they may only spend a few hours actually working with their mentor, in comparison to the multiple years of research expertise, coursework, and forming professional relationships. This might not be enough to change the outcome of a very noisy process.
Challenges in evaluating mentorship programs
We would like to answer the question, does participation in a mentorship program help students be admitted to graduate programs?
However, there are many challenges to evaluating the impact and efficacy of mentorship programs.
-
Confounding factors. There are many factors that make it more difficult for underrepresented students to be admitted, not just the lack of mentorship. Thus a student from an underrepresented background may be less likely to be admitted than a student from a privileged background, even if they both have access to mentorship.
-
Selection bias. We might look at the admission rate of students who participate in the mentorship program compared to similar students who do not participate. However, the decision to seek out and participate in a mentorship program may indicate that the student is already more "attuned" to graduate school applications and may be already more likely to be admitted regardless of their participation.
-
Privacy and confidentiality. If a student participates in a mentorship program that is targeted at certain groups, such as LGBTQ+ individuals, then revealing their participation would be outing them in a sensitive context. For this and other reasons, programs like EECS GAAP make strict pledges to preserve the privacy and confidentiality of students. For example, we commit to never sharing any information about participants in our program with the EECS Department or the EECS Graduate Office without their explicit consent. (Which in turn, we only asked for one time, which was to share with administrative staff to process application fee reimbursements.) And to certainly never share this information with any faculty or staff involved in the admissions process.
-
Application noise. It's really hard to get into graduate programs (admission rates at MIT EECS are in the 6-8% range). Even the strongest applicants can never be guaranteed of admission. And students might be rejected at one department but accepted at another for what is basically random chance, such as the timing of grant funding in different labs and the assignment of application files to different readers. Our numerators (number of students admitted) will be small.
Ultimately, this means that even computing the admission rate of participants in our program is a challenge, let alone doing any causal inference.
One solution
I recently came up with one method that would help conduct a robust analysis of the causal impact of participating in a mentorship program on admissions, addressing the challenges above. This method has some drawbacks but would be a valuable tool for program designers.
Here is the outline of the method.
-
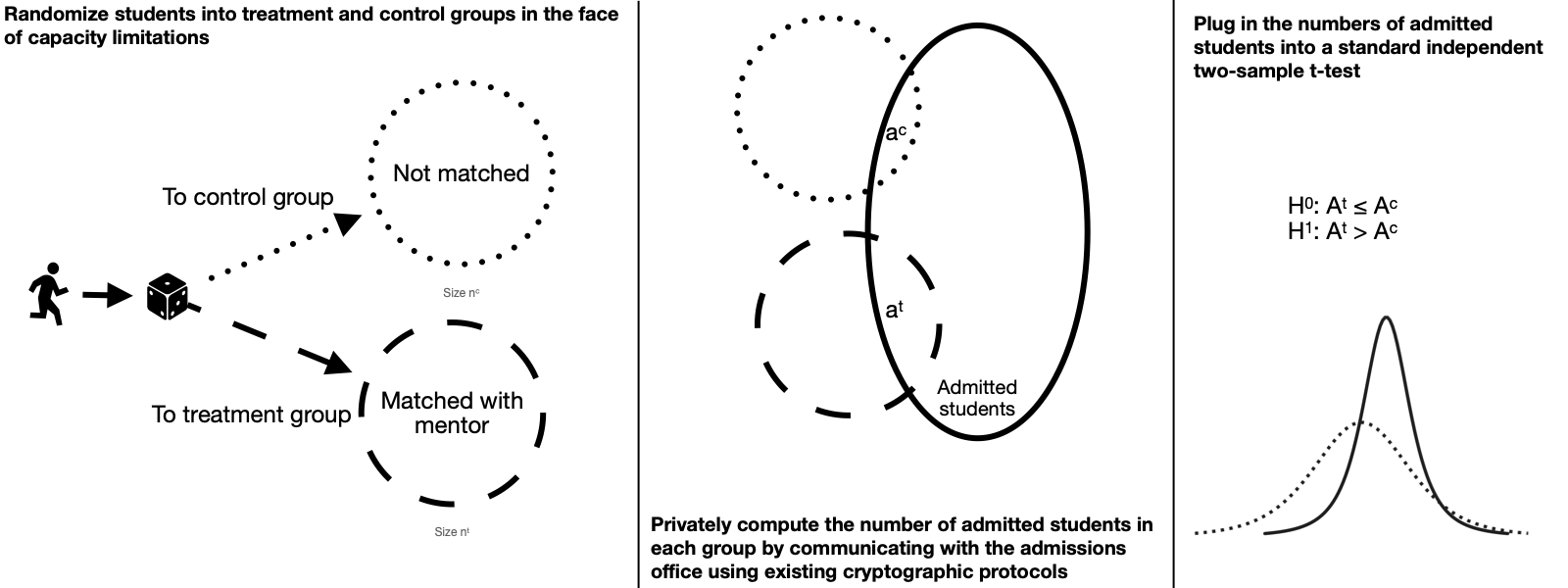
Form treatment and control groups by randomly accepting students into the mentorship program in the face of capacity limitations.
-
Measure outcomes of interest (such as admission rates) between the treatment and control groups by privately and securely comparing the participant lists with admissions records.
-
Plug these outcomes into basic statistical tests to determine the effect of the treatment.
Read on to see more of the technical details.
Preliminaries
Let $n$ be the number of students who apply to participate in the program. Let $n^t$ be the number of students who can be matched with mentors in the program (due to a limited number of mentors who are volunteering). Assume that if a student can't be offered a mentor, they will receive no other support from the program.1 Thus let $n^c$ be the number of students who are not offered mentors, and $n^t + n^c = n$.
Control groups
If a student is deemed to be eligible to the program, then accept them at random with probability $\frac{n^t}{n}$. This leads to a treatment group (offered a mentor) of size $n^t$ and a control group (not offered a mentor) of size $n^c$. Given this randomization, we can assume that latent characteristics of the two groups are similar.
We know $n^t$ exactly at the beginning of the program, but will have to estimate $n$. One approach is to carry forward the previous year's number of applications. Another approach is to use $2*n^t$ to form groups of equal size. If there are additional students who arrive "late" (beyond the number of students expected), then they have to be rejected anyway (there are still no more mentors) but they should not be included in the control group because their characteristics may be different. If $n$ is smaller, then the mentors can be matched more quickly and the pairs can get to work sooner.
Secure computation of admissions numbers
We now care about the following quantities:
| Value | Description |
|---|---|
| $s^t$ | the number of students in the treatment group who actually submit their application to the department |
| $s^c$ | the number of students in the control group who actually submit their application to the department |
| $a^t$ | the number of students in the treatment group who are admitted to the department |
| $a^c$ | the number of students in the control group who are admitted to the department |
| $e^t$ | the number of students in the treatment group who enroll in the department |
| $e^c$ | the number of students in the control group who enroll in the department |
If had these values, we could plug them into statistical tests to see the difference between treatment and control groups. But it's not so easy to do so without violating the privacy and confidentiality of the students.
-
Can we just send our list of treatment and control students to the admissions office? No, this would violate the confidentiality of students.
-
Can the admissions office send us the admissions results? No, academic departments treat admissions data as highly sensitive and would never share this with a student group.
-
Can students self-report participation in the mentorship program via a checkbox on the departmental application? No, we'd expect some non-response from participants due to privacy concerns, and even more non-response from the control group. You'd just be asking students to violate their own confidentiality. The resulting data would not be representative.
To address this, we can use algorithms for private set intersection (PSI), with modifications for private set intersection cardinality (PSIC), given that we do not need to know the intersecting elements but just their count.
This is not my area of expertise, but I did a brief literature review, and found that there are many algorithms for PSI. Applications include private contact list discovery and private advertising conversion detection.
For example, Freedman, Nissim, and Pinkas present a variety of protocols for private matching including derivative problems like private set intersection cardinality (which they call private cardinality matching). These protocols are based on existing homomorphic encryption systems, which are cryptosystems that preserve the group homomorphism of addition and allows multiplication by a constant. Preserving the group homomorphism of addition means that given Enc($m_1$) and Enc($m_2$), the encryptions of two secret values, one can efficiently compute Enc($m_1 + m_2$) without knowledge of the private key. Preserving multiplication by a constant is defined similarly. The elements in the set are encoded in a domain of a fixed size and then represented as the roots of a polynomial. The coefficients of the polynomial are encrypted and sent to a counterparty, who does some additional operations involving evaluating the polynomial on their own inputs, multiplying and adding by carefully chosen values, and encrypting the result. The cardinality protocol is described in Section 4.4 of the paper.
Much recent work (using improved techniques compared to homomorphic encryption) seems to focus on providing efficient algorithms, securing against malicious actors, or supporting multiple parties. We have a very simple use case with a small dataset (on the order of thousands), no malicious actors, and only two parties.
There are several open-source implementations of PSIC protocols. For example, Garimella et al provide a C++ implementation of PSIC (as well as other functions of the intersection) based on oblivious transfer that can compute the cardinality of intersection on $2^{12}$ = 4,096 items in around 8 seconds with about 3MB of communication. (There were 3,742 applicants to MIT EECS in 2020). OpenMined/PSI also implements PSIC based on elliptic-curve Diffie-Helman and Golomb-coded sets (but does not include a reference to a proof of security). I'm sure there are other implementations that I didn't find in my limited search.
You could argue that these private computational protocols are an over-engineered solution. You might be right. We could probably contract some law firm or trusted third party who could compare the sets of names directly. Yet this would still violate our promises of confidentiality. And given the sensitivity of the admissions data, it is unlikely such a party could be agreed upon.
Statistical tests
Let's focus on the outcome of admissions, but we can repeat the same analysis for other outcomes. Let $A^t$ be a random variable equal to $1$ if a treated student is admitted and $0$ otherwise, and let $A^c$ be a corresponding random variable for control students. The null hypothesis is that the means of $A^t$ and $A^c$ are identical, i.e. that there is no difference in the admission rate between GAAP participants vs a control group with similar characteristics.
We have that $\bar{A^t} = \frac{a^t}{n^t}$ is the sample mean of $A^t$ and $\bar{A^c} = \frac{a^c}{n^c}$ is the sample mean of $A^c$. We can reasonably assume that the variance of $A^t$ and $A^c$ are similar. Thus we can use a simple independent two-sample t-test.
The test statistic $t$ is given by
$$ t = \frac{ \frac{a^t}{n^t} - \frac{a^c}{n^c} }{ s_p \cdot \sqrt{\frac{1}{n^t} + \frac{1}{n^c}} } $$
where
$$ s_p = \sqrt{\frac{(n^t-1) s^2_t + (n^c-1) s^2_c}{n - 2}} $$
is an estimator of the pooled standard deviation of the two samples.
Now we can obtain standard p-values from $t$.
Using SciPy:
from scipy.stats import ttest_ind_from_stats
mean_t = a_t/n_t
mean_c = a_c/n_c
std_t = mean_t * (1-mean_t) ** 2 + (1-mean_t) * mean_t ** 2
std_c = mean_c * (1-mean_c) ** 2 + (1-mean_c) * mean_c ** 2
t, p = ttest_ind_from_stats(mean_t, std_t, n_t, mean_c, std_c, n_c)
Some hypotheses
This method is one way of evaluating the impact of mentorship on admissions outcomes. Now, to be clear, EECS GAAP has not implemented this method, nor did we have a program structure in our first year that would allow us to implement this even if we had wanted to. So without having done this analysis, I will pre-register hypotheses about how I think mentorship programs
I'll now pre-register hypotheses without having done this type of analysis.
H1: $A^t > A^c$. ("Students who receive mentorship are likely to be admitted at a higher rate than those who do not.") This is the most important hypothesis. If not, the fundamental thesis of application assistance programs is basically wrong and it's difficult to justify the effort put into the program.
H2: $S^t > S^c$. ("Students who receive mentorship are likely to submit their applications at a higher rate.") If this hypothesis is not confirmed, it's not a big deal. One could obtain this result without using expert mentors (i.e. the nagging parents effect). It could also be that students realize through working with their mentors that the program is not the right fit for them for whatever reason and they should focus their efforts elsewhere.
H3: $E^t = E^c$. ("Among all students who are admitted, students who had received mentorship enroll at the same rate as those who did not.") That is, I don't think the null hypothesis will be rejected that there was no effect on enrollment yield. I do think that there is an effect of mentors in "selling" the institution and in making applicants feel like they have a more personal connection. However, I think that there are other really strong factors that lead students to choose certain schools so this effect may not dominate. Also, this is where other DEI efforts should come into play (generally creating a more inclusive campus, having programming at visit days targeted to underrepresented students, etc.).
Drawbacks and limitations
There are several drawbacks to this method that program designers should consider carefully.
-
Capacity limitation. This method piggy-backs on the fact that a program may only be able to serve a limited number of applicants in order to create a control group. However, if there is no capacity limitation, then ethically a program should probably serve all eligible students rather than artificially introducing a limit in order to form a control group.
-
Random prioritization. To form a valid control group, applicants should be randomly assigned to be either accepted and matched with a mentor or to be rejected. However, this conflicts with other approaches to prioritization in the face of capacity limits, such as prioritizing based on underrepresented background (i.e., some backgrounds may be "more underrepresented" than others).
-
Timing effects. It would be great if all eligible students applied to the program at the beginning of the application cycle. In reality, students begin their graduate school applications at different points, and may find out about the mentorship program at different points during the cycle. If students arrive to the program consistently throughout the cycle, then randomly accepting a student conflicts with first-come-first-served approaches. While in one sense it is equally arbitrary to accept a student at random or due to when they happen to submit some application form, the end result is still that each applicant/mentor pair has less time to work together, on average.
-
Secondary support. In EECS GAAP at MIT, once we had matched all available mentors with applicants, we scrambled to support the students who continued applying to our program with other types of resources including group programming. Thus instead of turning away students to form a control group, a program may want to accept them but offer similar resources. In that case, our method would be comparing the efficacy of one-on-one mentoring versus the other resources, which is not quite what we are interested in. Some resources like application support materials may also be made available to the applicants with mentors which would partially alleviate this concern, yet they may take advantage of it differentially (i.e. pay less attention to a FAQ section in a document if they can just bounce questions off of their mentor directly).
There may be a fundamental tension between trying to help all students and trying to evaluate impact in a rigorous manner. But perhaps these secondary support resources offered by mentorship programs are not all that different from what students can find elsewhere on the internet, such that the evaluation methodology would still be valid. And I'd argue that students are better off in the long run if we can (1) conclusively show that mentorship programs are effective and use that to invest significantly more resources in them or (2) conclusively show that mentorship programs are not effective and shift our resources to other types of application support and DEI work.
-
Application fees. Many application assistance programs including EECS GAAP at MIT are able to raise money in order to pay the application fees of students who participate in the mentorship program. If this were only offered to the treatment group, it would obviously bias the results of the application submission comparison and would indirectly bias the results of the admission comparison. Program designers can address this by politely declining some students (when they are assigned to the control group) but still offering to pay their application fee. Graduate student labor is generally a more scarce resource that money.
Qualitative outcomes
We may also like to answer other questions about the effects on applicants and mentors in more qualitative outcomes like sentiment towards graduate school, confidence in application materials, and connectedness to the community. In EECS GAAP, these qualitative outcomes were what we most closely focused on, partly because we were more easily able to measure them, and because there is so much noise in the admissions process. There are challenges in evaluating these outcomes as well, which are usually assessed from surveys. These include "differential attrition," low response rates, and response linking.
Conclusion
The organizers of application assistance programs should evaluate the impacts of their program and be open to the negative finding that such programs do not positively influence admissions outcomes. The method described here is one way of rigorously evaluating this.
At EECS GAAP, we did use the best available data to evaluate our impact on admissions outcomes. I'm not able to share any findings due to the sensitivity of the data and informality of our analysis. I hope in the future that EECS GAAP or other mentorship programs can more publicly share such analysis.
Have you seen research evaluating the impact of mentorship programs in admissions? Do you have any feedback on the method in this post? Want to talk more about implementation? Let me know in the comments.
-
This was not true about EECS GAAP, because we did offer other resources or group programming to eligible students. ↩